Sparse-Input Neural Network Augmentations for Differentiable Simulators

Abstract

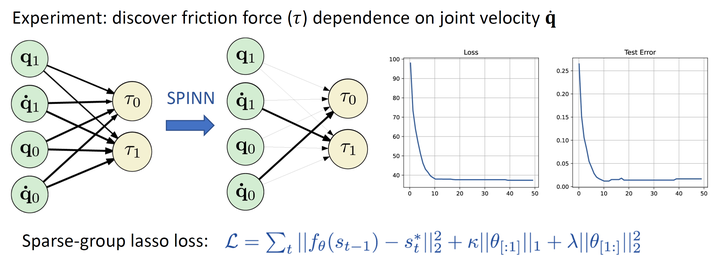
Differentiable simulators provide an avenue for closing the sim2real gap by enabling the use of efficient, gradient-based optimization algorithms to find the simulation parameters that best fit the observed sensor readings. Nonetheless, these analytical models can only predict the dynamical behavior of systems they have been designed for. In this work, we study the augmentation of a differentiable rigid-body physics engine via neural networks that is able to learn nonlinear relationships between dynamic quantities and can thus learn effects not accounted for in the traditional simulator. By optimizing with a sparse-group lasso penalty, we are able to reduce the neural augmentations to the necessary inputs that are needed in the learned models of the simulator while achieving highly accurate predictions.